数据结构(1)基础知识
数据结构
1 | 数据结构 |
概念
数据结构是为了方便对数据进行操作而设计的一种组织形式。它可以用来表示不同的数据类型,并提供各种操作方法,例如插入、删除、搜索、排序等。在计算机程序中,数据结构扮演着非常重要的角色,因为程序需要处理大量的数据并对其进行高效的操作。
数据结构是把数据元素按照一定的关系组织起来的集合,用来组织和存储数据
数据结构描述数据元素的组织方式和对其进行操作的方式,而ADT定义一组操作及其规范性行为,从程序设计者的角度来看待数据类型。
常见的数据结构有数组、链表、栈、队列、树、图等,它们具有不同的特点和应用场景。
1 | 在计算机中,不同的数据类型(如整型、浮点型、字符型等)将数据表示为特定的比特组合方式,从而赋予其特定的实际意义和用途。例如,在32位整型中,采用二进制补码表示负数,而对于单精度浮点型,使用指数表达科学计数法。 |
学习数据结构可以帮助你更好地理解和设计计算机程序,提高程序效率和可维护性。
计算机中的所有数据实例均由二进制字符串来表达。为了赋予这些数据实际的意义,必须要有数据类型。数据类型能够帮助我们解读二进制数据的含义,从而使我们能从待解决问题的角度来看待数据。这些内建的底层数据类型(又称原生数据类型,比如python的int())提供了算法开发的基本单元。
ADT(抽象数据类型)定义了一组操作,这些操作可以在不考虑实现细节的情况下执行。换句话说,ADT只关注数据类型的行为和语义,而不关心它的内部实现。因此,ADT提供了一个高层次的视角来描述数据类型,使得程序员不必了解其底层实现即可使用它们。例如,队列、堆栈、集合等都是ADT。
为了控制问题及其求解过程的复杂度,使用过程抽象的将细节隐藏起来(python的input()函数),数据抽象的基本思想与此类似,抽象数据类型(ADT)从逻辑上描述了如何看待数据以及其对应运算而无需考虑实现。
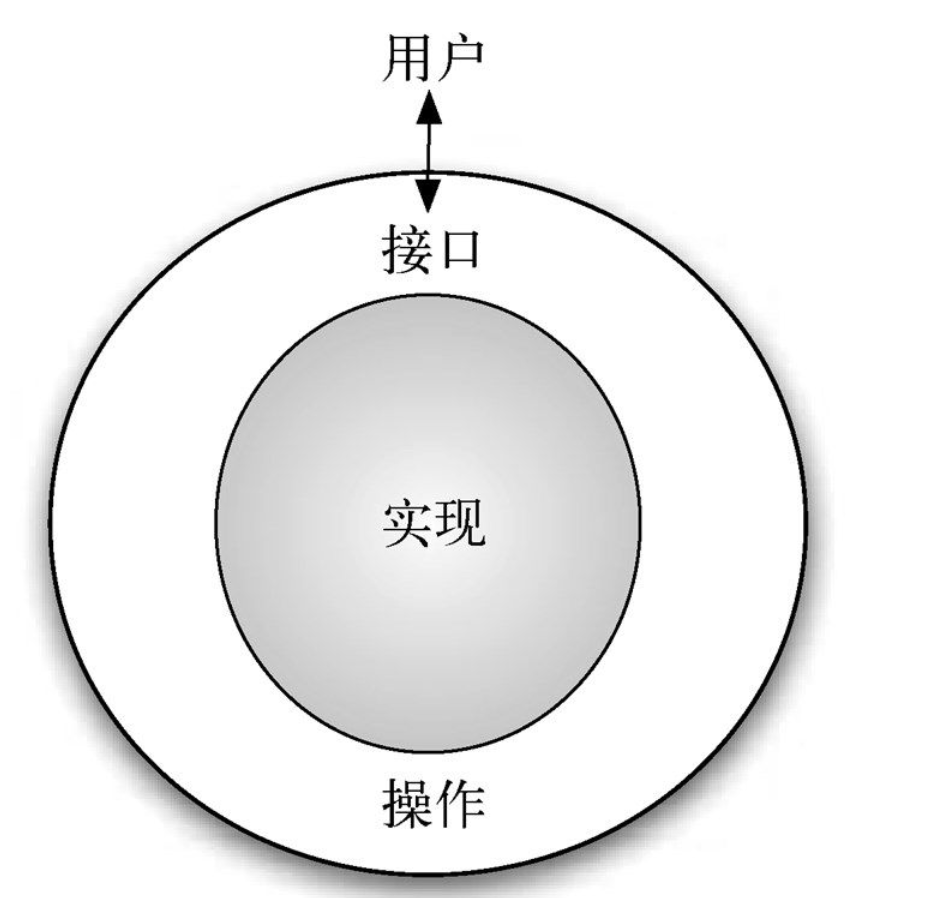
该抽象对数据进行封装提供了接口,这称为信息隐藏
而抽象数据类型的实现称为数据结构
eg.实现stack的ADT
在ADT的描述中,栈(Stack)是一种后进先出(Last-In-First-Out,LIFO)的抽象数据类型,只允许在一端进行插入和删除元素的操作,该端称为栈顶(top)。栈可以用顺序存储结构(即数组)或链式存储结构来实现,它的主要操作如下:
- push(item):将元素item压入栈顶
- pop():删除并返回栈顶元素
- top():返回栈顶元素
- is_empty():判断栈是否为空
下面是用Python列表来实现栈的ADT:
1 | class Stack: |
在这个Stack类中,我们使用Python列表来存储栈的元素,此处的列表可以看作是数组,用列表的append和pop方法来进行元素插入和删除操作,用len方法来判断栈是否为空,用最后一个元素的索引来查看栈顶元素。通过这些方法,我们实现了栈的ADT。用户只需要调用栈的方法就可以对栈进行操作,而不需要关心具体的实现细节。
术语
- 数据元素:指一个数据结构中的基本单位,也可以称为节点、元素、项等。每个数据元素包含若干个数据项(属性),用来描述某个实体或对象。
- 数据结构:指不同类型数据元素之间的关系,以及对这些元素进行操作的方法集合。常见的数据结构包括数组、链表、栈、队列、树、图等。
- 线性结构:指数据元素之间存在线性关系(即一对一的关系),例如数组、链表、栈和队列等。
- 非线性结构:指数据元素之间不存在简单的线性关系,例如树、图等。非线性结构通常具有层次性或者网状性。
- 子结构:指一个数据结构中的某个部分,可以看做是一种相对独立的小型数据结构,例如树的子树、链表的子链等。
- 抽象数据类型(ADT):指数据类型的抽象表示,它定义了数据元素的集合、数据元素之间的逻辑关系以及对数据元素的基本操作。ADT与具体实现没有关系,只关注数据类型本身的特征和操作。
- 栈:指一种先进后出(LIFO)的数据结构,只允许在栈顶进行插入和删除操作。
- 队列:指一种先进先出(FIFO)的数据结构,只允许在队尾进行插入操作,在队头进行删除操作。
- 树:指一种层次结构的数据结构,由若干个节点和边组成。其中,根节点没有父节点,其他节点都有唯一的父节点,可以有零个或多个子节点。
- 图:指由若干个节点和边组成的数据结构,其中每个节点表示一个数据元素,每条边表示节点之间的关系。
python基础
python支持面向对象编程,类都是对数据的构成(状态)以及数据能做什么(行为)的描述。
类与抽象数据类型相似,在面向对象编程范式中,数据项被称为对象,一个对象就是一个实例。
内建原子数据类型
python提供了两大内建数据类实现了int类型和float类型可以进行标准的数学运算
1 | >>> 2+3*4 |
python通过bool类实现布尔数据类型
1 | >>> False |
标识符在编程语言中被用作名字。python中的标识符以字母或下划线开头区分大小写,任意长度。
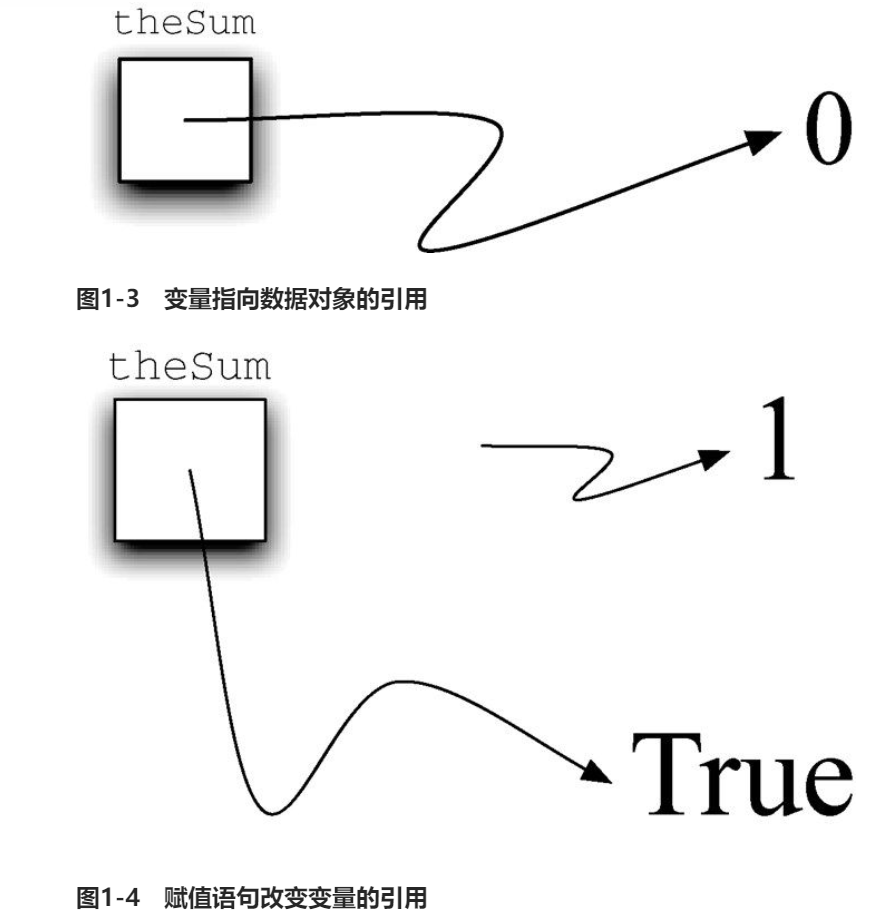
当一个名字第一次出现在赋值语句左边,会创建对应的python变量。赋值语句将名字和值关联起来。
python先计算右侧的表达式,然后判断数据类型并赋值给变量,体现了python的动态特性
变量存储的时指向数据的应用,而不是数据本身,类似一个内存指针
内建集合数据类型
列表、字符串以及元组时概念上非常相似的有序集合。集(set)和字典时无序集合。
列表
列表是零个或多个指向Python数据对象的引用的有序集合,通过在方括号内以逗号分隔的一系列值来表达。空列表就是[]。
列表是异构的,一个列表中可以包含不同类型的元素,这些元素的数据类型可以不同
1 | >>> [1,3,True,6.5] |
由于列表是有序的,它支持一系列可应用与任意python序列的运算
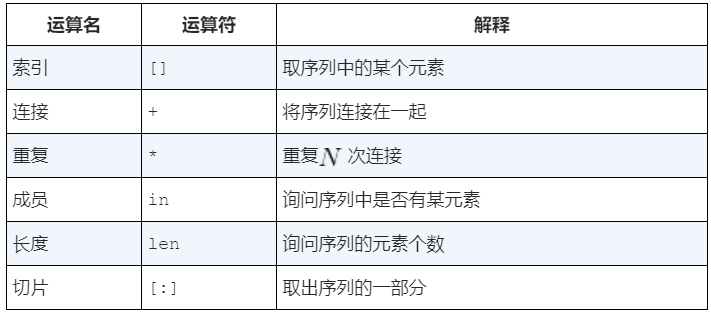
列表和序列的下表从0开始。mylist[1:3]会返回一个下标从1到2的元素列表并没有包含3,
需要快速初始化列表可以通过重复运算来实现
1 | mylist=[0]*6 |
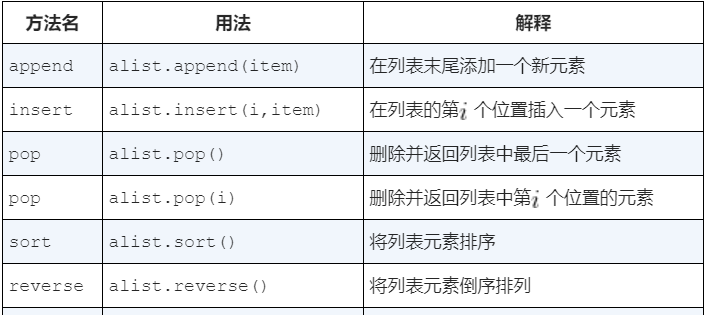
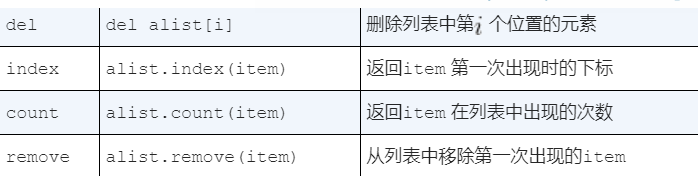
1 | >>> myList |
句点符号mylist.sort()用来调用某个对象的方法,请求mylist调用其sort方法并传入空的参数。
range()会生成一个代表值序列的范围对象。使用list函数,能够以列表形式看到范围对象的值
1 | >>> range(10) |
字符串
是零个或多个字母、数字和其他符号的有序集合。这些字母、数字和其他符号被称为字符。常量字符通过引号和标识符进行区分
1 | >>> "David" |
python字符串的方法
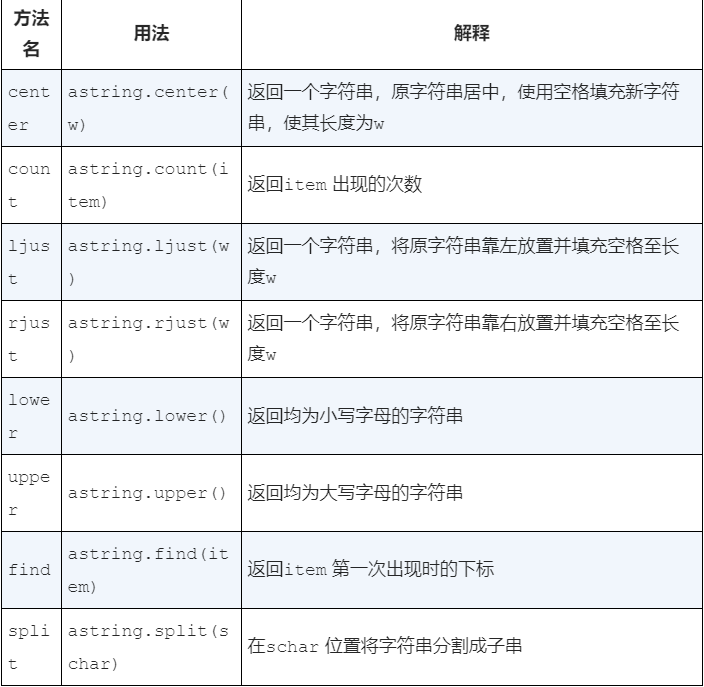
1 | >>> myName |
列表和字符串的主要区别在于,列表可以修改字符串不能。列表的这一特性叫可修改性
元组
由于都是异构数据序列,因此元组和列表非常相似
他们的区别在于,元组和字符串一样不可修改,元组通常写成由括号并且以逗号分隔的一系列值,与序列一样,元组允许和字符串一样的任何操作
1 | >>> myTuple = (2,True,4.96) |
元组和字符串是两种不同的数据类型,它们有以下区别:
- 可变性:字符串是不可变的,即它们的值在创建后无法修改。而元组是可变的,虽然元组中的元素本身不可变,但是我们可以修改元组中元素的值或者增删元素。
- 数据类型:字符串是由单个字符组成的序列,而元组是由多个任意类型的元素组成的序列。因此,元组可以包含任何数据类型的元素,包括数字、字符串、列表、字典等。
- 表示方式:字符串用单引号、双引号或三引号表示,而元组使用圆括号表示。
- 用途:字符串常用于表示文本信息,如文件内容、用户输入、输出信息等。元组则常用于存储和传递数据,如函数返回多个值时,可以用元组来打包这些值并返回。
集(set)
由零个或多个不可修改的python数据对象组成的无序集合。集不允许重复元素,并且写成由花括号包含、以逗号分隔的一系列值。,空集set(),集也是异构的
1 | >>> {3, 6, "cat", 4.5, False} |
set支持的运算
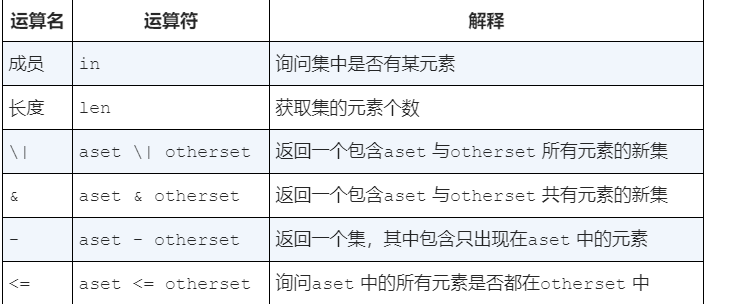
1 | >>> mySet |
set提供的方法
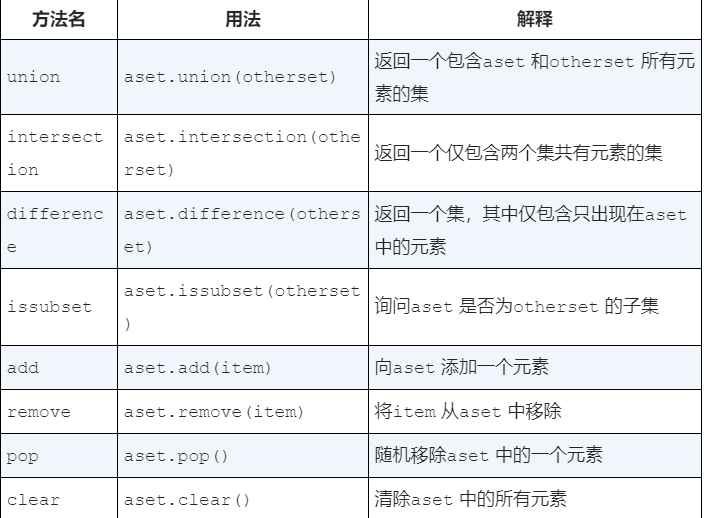
1 | >>> mySet |
字典
字典是无序结构,由相关元素对构成,其中每对元素都由一个key和一个value组成,写成key:value
字典由花括号包含一些列以逗号分隔的键值对表达
1 | >>> capitals = {'Iowa':'DesMoines','Wisconsin':'Madison'} |
访问字典通过key来访问
1 | >>> capitals['Iowa'] |
字典不是根据key来进行有序维护的,key的位置是由散列来决定的
字典的运算

字典的方法
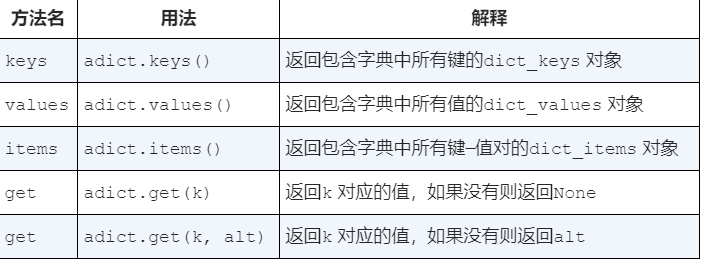
1 | >>> phoneext={'david':1410, 'brad':1137} |
输入和输出
input()
input()函数接受一个字符串作为参数。由于该字符串包含有用的文本来提示用户输入,因此它经常被称为提示字符串。
1 | aName = input('Please enter your name: ') |
input 函数返回的值是一个字符串,它包含用户在提示字符串后面输入的所有字符。如果需要将这个字符串转换成其他类型,必须明确地提供类型转换。在下面的语句中,用户输入的字符串被转换成了浮点数,以便于后续的算术处理。
1 | sradius = input("Please enter the radius of the circle ") |
print()
print 函数为输出Python程序的值提供了一种非常简便的方法。它接受零个或者多个参数,并且将单个空格作为默认分隔符来显示结果。通过设置sep 这一实际参数可以改变分隔符。此外,每一次打印都默认以换行符结尾。这一行为可以通过设置实际参数end 来更改。下面是一些例子。
1 | >>> print("Hello") |
格式化运算符
格式化字符串是一个模板,其中包含保持不变的单词或空格,但是年龄名字会根据运行变量变化
1 | print("%s is %d years old." % (aName, age)) |
%是字符串运算符,称为格式化运算符,表达式左边是模板,邮编是用于格式化字符串的值,邮编的值的格式与格式化字符串中的%的个数一致,这些值将依次从左到右地被换入格式化字符串中。
格式化字符串包含一个或多个转换声明,转换字符告诉格式化运算符,什么类型的值会被插入到字符串中的相应位置,在上面%s声明了一个字符串,%d声明了一个整数
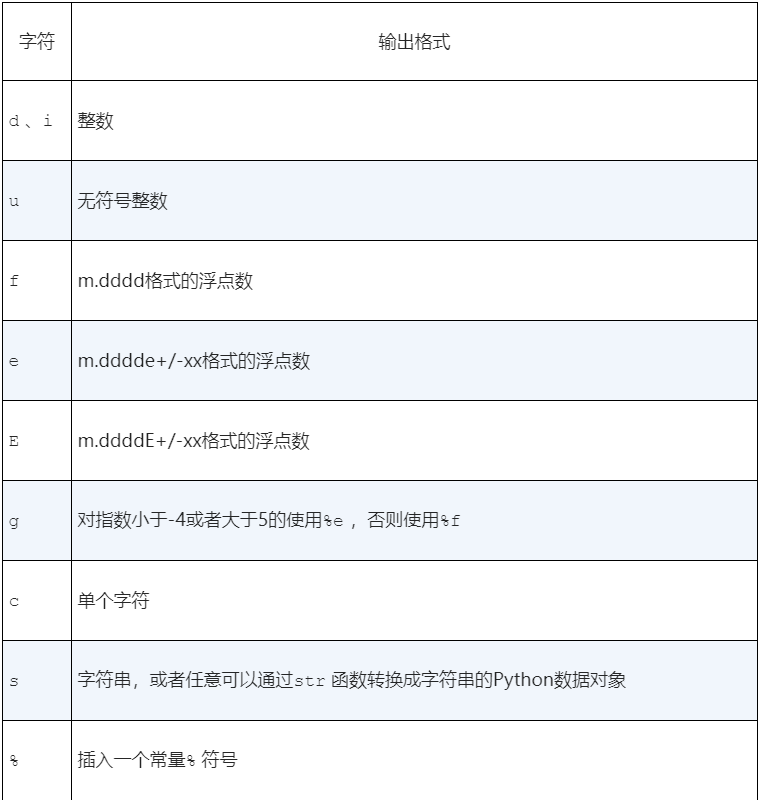
在%和格式化字符之间加入一个格式化修改符,可以根据给定的宽度进行左对齐或者右对齐,也可以通过小数点之后的一些数字来之指定宽度
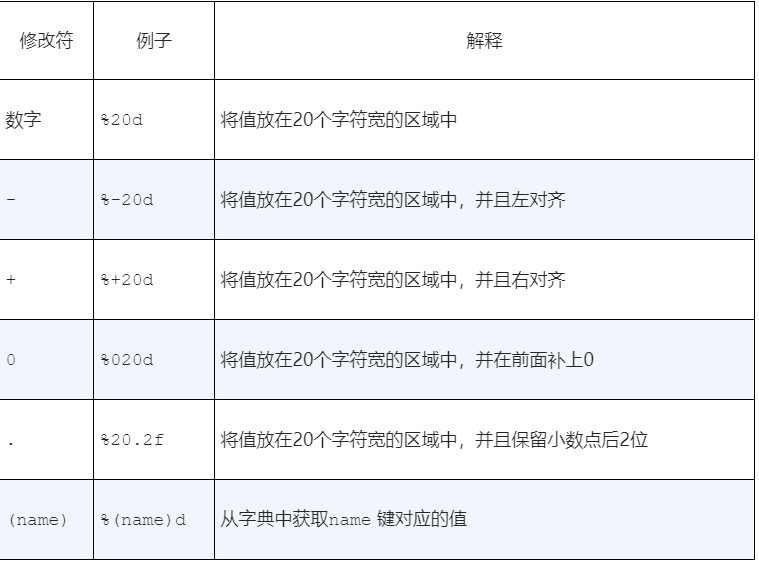
格式化运算符的邮编是被插入格式化字符串的一些值,这个集合可以是元组或者字典,如果是元组则根据位置次序插入,如果是字典,那么根据对应的简直插入,并且所有格式化字符串必须使用nae修改符号来指定键名
1 | >>> price = 24 |
Python的字符串还包含了一个format 方法。该方法可以与新的Formatter 类结合起来使用,从而实现复杂字符串的格式化。可以在Python参考手册中找到更多关于这些特性的内容。
控制结构
while
在给定条件位true时无限循环。
for
用于遍历一个序列集合的每个成员
for 语句的另一个非常有用的使用场景是处理字符串中的每一个字符。
列表解析式
列表可以通过迭代结构和分支结构来创建
1 | >>> sqlist = [x*x for x in range(1,11)] |
变量x 会依次取由for 语句指定的1到10为值。之后,计算x*x 的值并将结果添加到正在构建的列表中。列表解析式也允许添加一个分支语句来控制添加到列表中的元素,如下所示。
1 | >>> sqlist = [x*x for x in range(1,11) if x%2 != 0] |
异常处理
在编程中常遇到语法错误或者逻辑错误,这些称为异常
党异常发生我们称抛出异常,可以用try来处理
try语句调用print来处理异常,对应的except遇见捕捉这个异常
例如,以下代码段要求用户输入一个整数,然后从数学库中调用平方根函数。如果用户输入了一个大于或等于0的值,那么其平方根就会被打印出来。但是,如果用户输入了一个负数,平方根函数就会报告ValueError 异常。
1 | >>> anumber = int(input("Please enter an integer ")) |
except 会捕捉到sqrt 抛出的异常并打印提示消息,然后会使用对应数字的绝对值来保证sqrt 的参数非负。这意味着程序并不会终止,而是继续执行后续语句。
1 | >>> try: |
定义函数
def 函数(),可以通过这个隐藏计算细节
1 | >>> def square(n): |
定义类
每当需要实现抽象数据类型时,就可以创建新的类
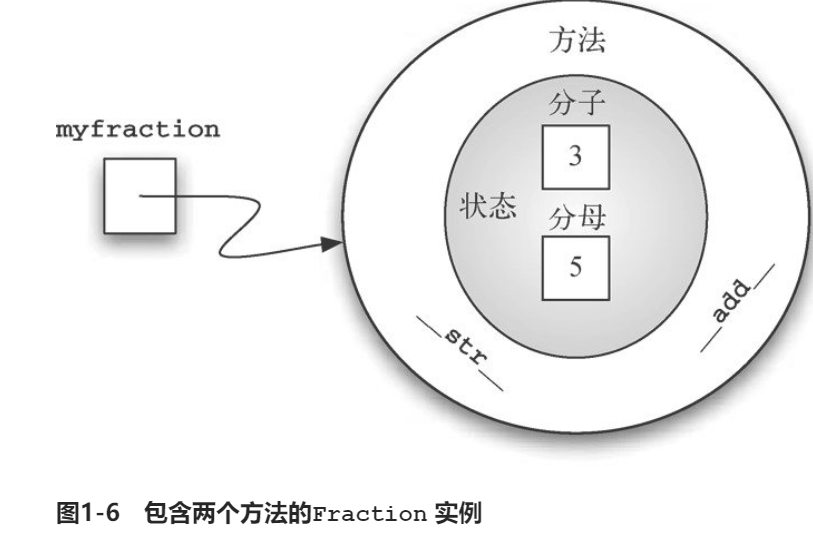
Fractioni类
Fraction 类是 Python 标准库中的一个类,用于表示分数。Fraction 类可以将分数表示为一个分子和一个分母的元组,同时还提供了一系列方法,用于对分数进行运算。
重现部分功能
1 | class Fraction:#定义一个类 |
继承:逻辑门与电路
继承:使一个类与另一个类相关联,python中的子类可以从父类继承特征数据和行为。父类也称为超类。
下图的结构称为继承层次结构
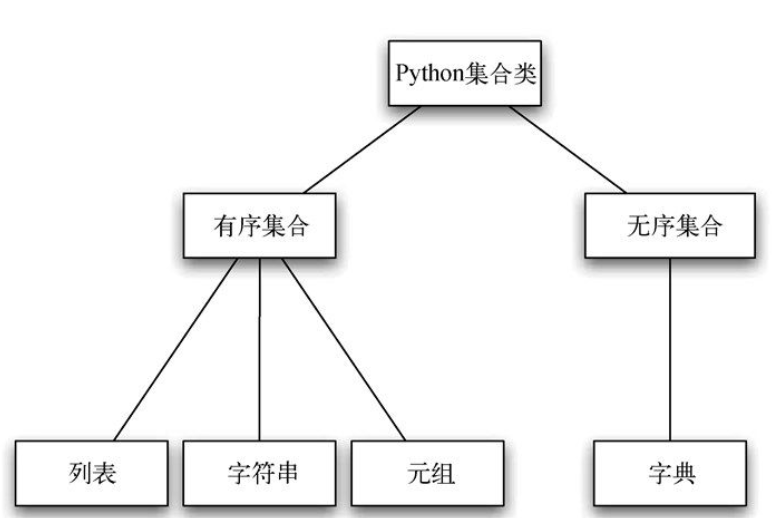
列表是有序集合的子,因此,我们将列表称为子,有序集合称为父(或者分别称为子类列表和超类序列)。这种关系通常被称为IS-A关系 (IS-A意即列表是一个 有序集合)。
实现下面这个
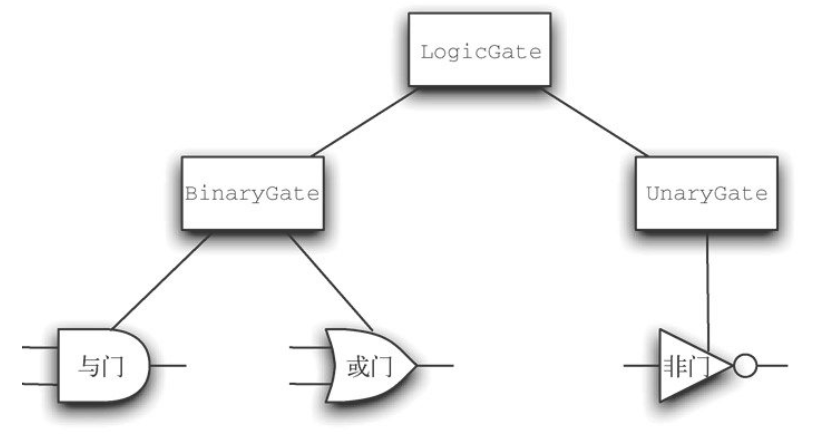
1 | class LogicGate: |
算法(Algorithm)
定义
根据 Donald Knuth 的定义,算法(Algorithm)是指解决问题的一系列步骤,这些步骤按照一定的顺序执行,每个步骤都可以在有限的时间内完成,并能够产生某种输出结果。
另一位著名的计算机科学家 Thomas H. Cormen 等人给出的定义是,算法是一种精确定义的、确定性的、有效的、可行的、有穷的方法,用来解决特定问题的计算过程。
这两个定义都强调了算法必须具有准确的描述和明确的执行过程,而且必须能够在有限的时间内产生正确的输出结果。同时,算法也应该能够处理各种情况并能够适应不同规模的数据输入。
算法是为逐步解决问题而设计的一系列通用指令。给定某个输入,算法能得到对应的结果——算法就是解决问题的方法。
程序则是用某种编程语言对算法编码。同一个算法可以对应许多程序,这取决于程序员和编程语言。
特性
- 确定性:算法中的每个步骤都必须是精确而明确的,不会产生歧义或二义性。
- 有限性:算法必须在有限的时间内运行结束,不能无限制地执行下去。
- 输入:算法需要接收数据输入,并且必须能够处理各种情况和异常情况。
- 输出:算法应该能够产生输出结果,这个结果应该符合问题的要求和需求。
- 可行性:算法应该是可行的,即能够被实现并能够在给定的计算机环境下运行。
- 稳定性:算法应该能够在不同的输入数据下得到相同的输出结果,避免因输入数据的变化导致程序的错误。
- 高效性:算法应该尽可能高效,能够在较短的时间内执行完毕,并且占用较少的计算资源。
- 独立性:算法应该是独立的,即不受具体实现方式和编程语言的限制。
计算资源
大O记法
大O记法是用来描述算法效率的一种数学符号,通常用于衡量算法时间复杂度的上限。时间复杂度是一个函数f(n),表示算法执行的基本操作次数随着输入规模n的增加而增长的趋势。
常见的时间复杂度有:
- 常数时间复杂度(O(1))
- 对数时间复杂度(O(log n))
- 线性时间复杂度(O(n))
- 线性对数时间复杂度(O(n log n))
- 平方时间复杂度(O(n^2))
- 指数时间复杂度(O(2^n))
- 阶乘时间复杂度(O(n!))

算法性能有时不依赖于问题规模,还依赖于数据值。对于这种算法要用最坏情况、最好情况、普通情况来描述性能。
在计算时间复杂度时,我们通常考虑输入数据规模n对于算法运行时间的影响。因此,时间复杂度是一个函数f(n),表示算法执行的基本操作次数随着输入规模n的增加而增长的趋势。一般情况下,我们会将算法中最耗时的操作(通常是循环)的运行次数作为时间复杂度的基础。
需要注意的是,时间复杂度是一个渐进复杂度,即当n趋近于无穷大时,算法的运行时间会趋近于时间复杂度所代表的数量级。同时,时间复杂度只描述算法的执行时间,不考虑空间复杂度和其他因素。
1 | T(n)=5n^2 + 27n + 1005 |
例如这个例子,当n无限大时可以忽略其他留下影响最大的5n^2,当n再大系数5也没用了,所以f(n)=n^2,也可以写为O(n^2)
python数据结构的性能
列表
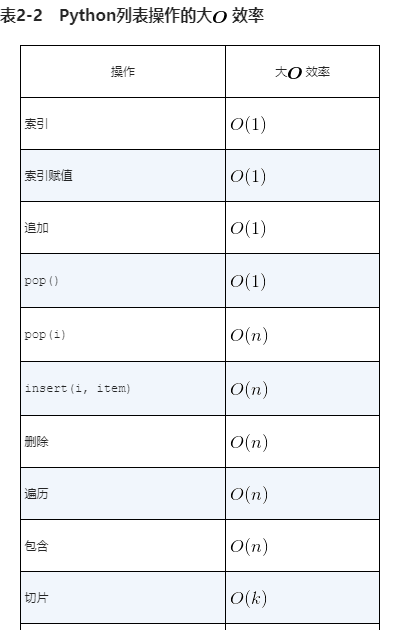
最常见的操作时索引和给某个位置赋值,无论列表长度这两个操作的所花的时间应该是恒定的。像这种与列表长度无关的操作就是常数阶的。O(1)
另一个常见操作时加长列表,由两种方式,要么追加,要么连接。追加方法是常数阶的。如果连接列表长度为k那么操作的时间复杂度就是O(K)

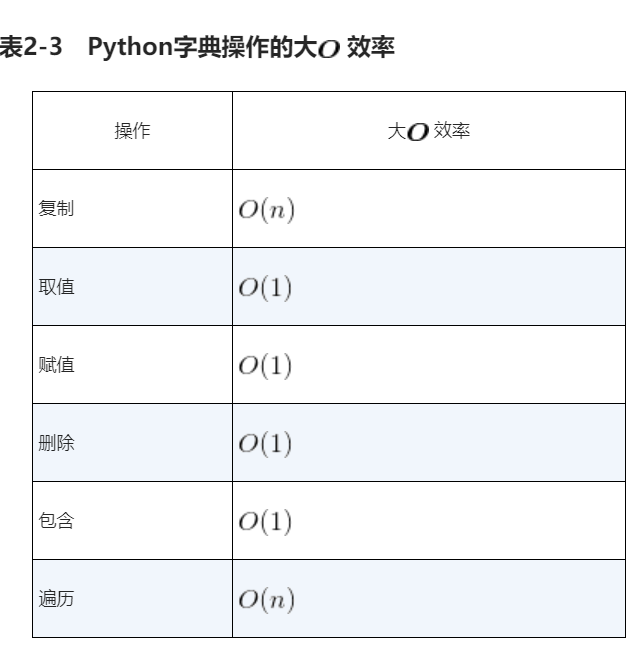
字典